Ein Schüler belegt mehrere Kurse, ein Kurs wird von mehreren Schülern besucht. Zwischen den Entitätstypen Schüler und Kurs besteht also eine wechselseitige Beziehung. Aus der Sicht eines Kurses gehören ihm einige Schüler an, aus der Sicht des Schülers müssen viele Kurse belegt werden, um den Verpflichtungen der Oberstufenverordnung zu genügen. Doch wie modellieren wir die Punktzahl, die ein Schüler in einem Kurs erhält?

Die Punktzahl kann kein Attribut des Entitätstyps Schüler sein, denn die Puntkzahl bezieht sich auf einen Kurs. Sie kann aber auch kein Attribut des Entitätstyps Kurs sein, denn sie bezieht sich immer auch auf einen Schüler. Die Punktzahl ist also ein Beziehungsattribut und wird daher mit der Beziehungsraute verbunden.

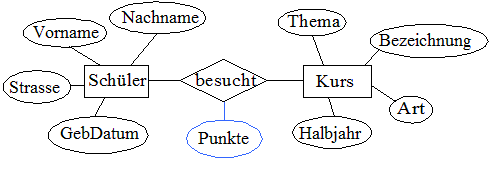
ER-Diagramm Schüler und Kurse mit Beziehungsattribut Punkte

Beziehungsdaten sind also eigenständige Daten. Ein guter Datenbankentwurf muss klar zwischen Daten über Entitätstypen und Beziehungen trennen.

Max Meier belegt den Kurs Q2 Datenbanken.

Schüler belegen Kurse.

Bei der objektorientierten Modellierung hatte eine Beziehung immer eine Richtung. Bei einer Datenmodellierung besteht der Zusammenhang zwischen zwei Entitätstypen in beiden Richtungen.

• ein Schüler belegt einen Kurs
• ein Kurs wird belegt von Schülern

Zur genauen Analyse einer Beziehung müssen beide Richtungen betrachtet werden.

Die Benennung einer Beziehung zwischen zwei Entitätstypen A und B ist so zu wählen, dass das nachfolgende Schema ein fehlerfreien Satz liefert:

Ein Lehrer   hat sich beworben an  einer Schule.
Eine Schule  hat                   einen Hausmeister.
Ein Ort      hat                   eine Schule.
Eine Schule  liegt in              einem Ort.

Darstellung der Beziehung

Eine Beziehung wird durch eine Raute dargestellt. Sie enthält oben die Benennung der Richtung A zu B, unten die Benennung der Richtung B zu A. Die Raute wird links/oben mit dem Entitätstyp A, rechts/unten mit dem Entitätstyp B verbunden.

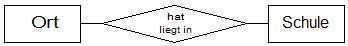
ER-Diagramm Ort hat/liegt in Schule mit Nennung beider Beziehungstyp-Richtungen

Beziehungen zwischen Entitätstypen weisen unterschiedliche Kardinalitäten auf. Die Beziehung zwischen Schüler und Kurs wird als m:n-Beziehung bezeichnet: Ein Schüler besucht mehrere (n) Kurse, ein Kurs wird von mehreren (m) Schülern besucht.

Die Lehrer hält Kurs Beziehung ist hingegen eine 1:n-Beziehung, weil ein Lehrer mehrere (n) Kurse hält, aber ein Kurs von einem (1) Lehrer gehalten wird.

Die Klassenlehrerbeziehung hingegen ist eine 1:1-Beziehung, denn eine Klasse hat einen Klassenlehrer und ein Lehrer hat eine Klasse.

Die Entscheidung über die Kardinalität einer Richtung der Beziehung wird über die sogenannte KaMe-Frage getroffen.

Ja    →  Kardinalität ist n
Nein  →  Kardinalität ist 1

Kann ein Mann mit mehreren Frauen verheiratet sein?  Nein, Kardinalität ist 1.
Kann ein Ort mehrere Schulen haben?                  Ja, Kardinaliät ist n.
Kann eine Schule in mehreren Orten liegen?           Nein, Kardinaliät ist 1.

Darstellung der Kardinalität

Die Kardinalität wird im ER-Diagramm mit 1, n oder m an das Ende der Beziehung geschrieben.

ER-Diagramm Ort hat/liegt in Schule mit Kardinalität der Beziehung

Grundsätzlich unterscheidet man drei Kardinalitätstypen:

eine 1:1-Beziehung
eine 1:n-Beziehung
eine n:m-Beziehung

Eine n:1-Beziehung wird auch als 1:n-Beziehung bezeichnet. Um deutlich zu machen, dass bei einer n:n-Beziehung unterschiedliche Anzahlen von Entitäten eine Beziehung eingehen können, spricht man von der n:m-Beziehung.

Mit der Optionalität einer Beziehung wird ausgedrückt, ob eine Entität eine Beziehung eingehen kann oder muss, ob diese Beziehung also optional oder obligatorisch ist. Beispielsweise ist die verheiratet-Beziehung zwischen Männern und Frauen optional, während die Tutor-Beziehung zwischen Schülern und Tutoren obligatorisch ist, denn jeder Schüler hat einen Tutor. Wie bei der Kardinaliät muss die Frage nach der Optionalität für beide Beziehungstyprichtungen geklärt werden.

MuMi-Frage

Die Entscheidung über die Optionalität einer Richtung der Beziehung wird über die sogenannte MuMi-Frage getroffen.

Ja     →   nicht optional, obligatorisch, muss-Beziehung
Nein   →   optional, nicht obligatorisch, kann-Beziehung

Muss ein Mann mit mindestens einer Frau verheiratet sein?  Nein, optional, kann-Beziehung
Muss ein Ort mindestens eine Schule haben?                 Nein, optional, kann-Beziehung
Muss eine Schule in mindestens einem Ort liegen?           Ja, obligatorisch, muss-Beziehung

Darstellung der Optionalität

Die Optionalität wird mit den Wörtern kann bzw. muss im ER-Diagramm an den Anfang der Beziehung geschrieben.

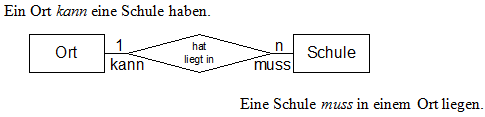
ER-Diagramm Ort hat/liegt in Schule mit Optionalität der Beziehung

1. Formuliere die Benennung der Beziehungen für ein oder mehrere der vier Miniwelten.

2. Formuliere die KaMe- und MuMi-Fragen für ein oder oder mehrere der vier Miniwelten.

3. Erweitere die ER-Diagramme der Miniwelten um die Angabe der Kardinalitäten und Optionalitäten.