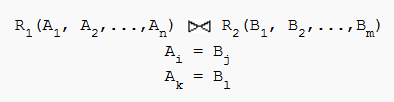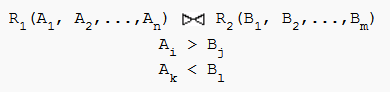Inhaltsverzeichnis
Relationenalgebra
Mit der Grundregel und den Regeln für 1:n- und 1:1-Beziehungen haben wir das Instrumentarium zur Verfügung mit dem ein ER-Diagramm auf Relationen abgebildet werden kann. Sind die Daten in Tabellen erfasst, so stellt sich nun die Frage, wie mit diesen Tabellen gearbeitet werden kann und wie mit Hilfe dieser Tabellen Datenbankabfragen realisiert werden können. Wir werden sehen, dass dazu drei Grundoperationen nötig sind:
- Selektion
- Projektion
- Join
Diese Grundoperationen werden auf Relationen angewendet und können zu mathematischen Termen kombiniert werden. Man spricht daher auch von der Relationenalgebra.
Selektion - Auswahl von Zeilen
Sei B eine Bedingung und R eine Relation. Die Bedingung B kann Konstanten und Attribute als Operanden, sowie Vergleichsoperatoren (<, ⇐, =, <>, ⇒, >) und logische Operatoren (and, or, not) enthalten. Dann ist die Selektion σB(R) die Menge aller Datensätze, die die Bedingung B erfüllen.
Beispiel
Gegeben ist die Relation KursLehrerRaum
| KursNr | Lehrer | Raum |
|---|---|---|
| 11 | Müller | 123 |
| 12 | Schulze | 124 |
| 27 | Bauer | 14 |
| 15 | Maier | 14 |
| 17 | Maier | 17 |
| 3 | Zange | 211 |
Die Selektion σKursNr > 15(KursLehrerRaum) erzeugt durch Streichung von Zeilen die Relation:
| KursNr | Lehrer | Raum |
|---|---|---|
| 27 | Bauer | 14 |
| 17 | Maier | 17 |
Projektion - Auswahl von Spalten
Gegeben sei die Relation R(A, B, C, D, E, F, …).
Dann ist πB, D, E, …(R) die Projektion von R auf die Attribute B, D, E, …
Duplikate müssen aus der projizierten Relation entfernt werden, denn mathematisch handelt es sich bei einer Relation um die Menge der Zeilen.
Beispiel
Gegeben ist die Relation KursLehrerRaum
| KursNr | Lehrer | Raum |
|---|---|---|
| 11 | Müller | 123 |
| 12 | Schulze | 124 |
| 27 | Bauer | 18 |
| 15 | Maier | 14 |
| 17 | Maier | 14 |
| 3 | Zange | 211 |
Die Projektion πLehrer, Raum(KursLehrerRaum) erzeugt durch Streichung von Spalten und Elimination der Doubletten die folgende Relation.
| Lehrer | Raum |
|---|---|
| Müller | 123 |
| Schulze | 124 |
| Bauer | 18 |
| Maier | 14 |
| Zange | 211 |
Datenbanksysteme entfernen standardmäßig keine Doubletten. Man muss dann spezielle Anweisungen zum Entfernen der Doubletten benutzen (z.B. SELECT DISTINCT)
Join - Verbinden von zwei Relationen
Bei der Abbildung eines ER-Diagramms auf Relationen werden Daten auf verschiedene Relationen verteilt. Mit der Join-Operation können zwei Relationen mit einem gemeinsamen Attribut zu einer Relation verbunden werden. In der Regel erfolgt die Verknüpfung über einen Primärschlüssel einer ersten Relation und den zugehörigen Fremdschlüssel in einer zweiten Relation. Der Join wird über drei Operationen berechnet: Kreuzprodukt der Relationen, Selektion und Projektion.
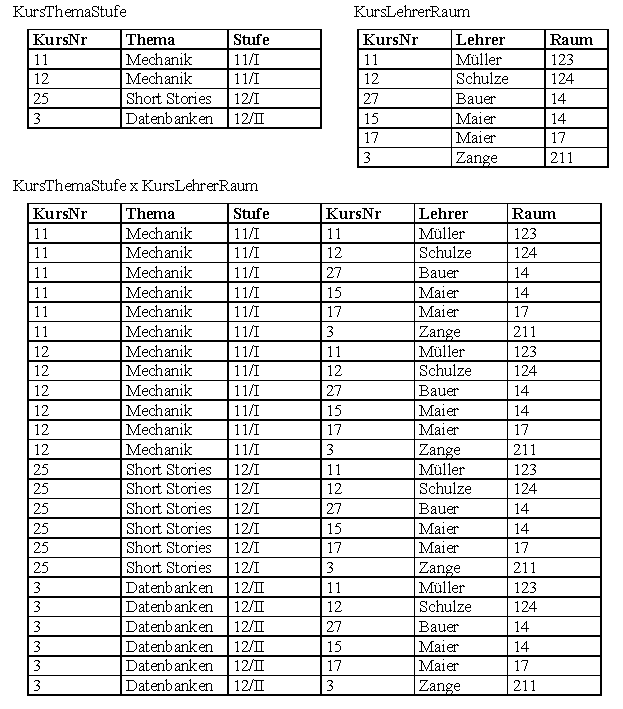
Kreuzprodukt
Beim Kreuzprodukt wird jede Zeile der ersten Relation mit jeder Zeile der zweiten Relation verbunden.
- Hat die erste Relation n Zeilen und die zweite m Zeilen, so besteht das Kreuzprodukt aus n*m Zeilen.
- Hat die erste Relation n Spalten und die zweite m Spalten, so besteht das Kreuzprodukt aus n+m Spalten.
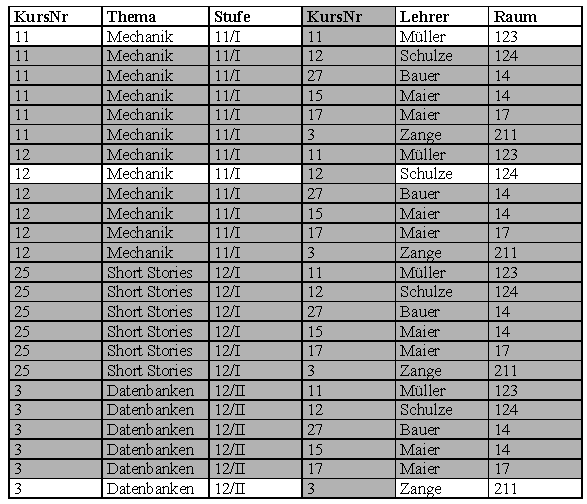
Selektion
Inhaltlich hat natürlich der Kurs 11 mit den Kursen 12, 27, 15, 17 und 3 nichts zu tun. Es interessiert eigentlich nur die Verbindung der Zeilen mit gleicher Kursnummer. Der Join macht daher als nächstes auf dem Kreuzprodukt eine Selektion über die gemeinsame Spalte bei gleichen Werten:
σKursThemaStufe.KursNr = KursLehrerRaum.KursNr(KursThemaStufe ⨉ KursLehrerRaum)
Projektion
Die gemeinsame Spalte KursNr wird in der Ergebnisrelation nur einmal benötigt, weswegen der Join zum Abschluss mit einer Projektion die zweite KursNr eliminiert.
Join
Als Ergebnis der drei Operationen (Kreuzprodukt, Selektion, Projektion) kommt der sogenannte Join (Zeichen: ⨝, Unicode U+2A1D) heraus. Wird das Join-Zeichen (Ersatzsymbol  ) bei älterer Software (z. B. Windows XP) nicht richtig angezeigt, so muss ein Zeichensatz, der Unicode-Zeichen darstellen kann, installiert werden (UTF-8-Probleme).
) bei älterer Software (z. B. Windows XP) nicht richtig angezeigt, so muss ein Zeichensatz, der Unicode-Zeichen darstellen kann, installiert werden (UTF-8-Probleme).
KursThemaStufe ⨝ KursLehrerRaum =
πKursNr, Thema, Stufe, Lehrer, Raum(
σKursThemaStufe.KursNr = KursLehrerRaum.KursNr(KursThemaStufe ⨉ KursLehrerRaum))
Der Join verbindet zwei Relationen über gemeinsame Spalten bei gleichen Attributwerten.
Join-Varianten
Den Join gibt es in verschiedenen Varianten. Grundlage aller Joins ist die Bildung des Kreuzproduktes der beiden beteiligten Relationen. Die Varianten unterscheiden sich hinsichtlich der Bildung der anschließenden Selektion.
Nur der Natural Join projiziert doppelte vorkommende Attribute aus. Alle anderen Joins führen keine Projektion aus. Dies führt zwangsläufig zu Namenskonflikten, denn wenn zwei Relationen gleichbenannte Attribute haben, so enthält deren Join gleichbenannte Attribute, wobei die Attributwerte durchaus unterschiedlich sein können. Auf einer solchen Relation sind die grundlegenden Operationen Selektion und Projektion nicht mehr definiert, weil man bei einem Bezug auf ein doppelt vorkommendes Attribut nicht entscheiden kann, welche Spalte gemeint ist.
Es gibt zwei Ansätze, dieses Problem zu lösen. Man kann erstens qualifizierende Attributnamen verwenden. Dabei ist der Join R1  R2 der beiden Relationen R1(A1, A2,…, An, B1, B2,…,Bk) und R2(C1, C2,…,Cm, B1, B2,…,Bk) mit k gleichbenannte Attributen B1, B2,…,Bk die Relation
mit den Attributen (A1, A2,…,An, R1.B1, R1.B2,…, R1.Bk, R2.B1, R2.B2,…,R2.Bk, C1, C2,…,Cm). Die Qualifizierung besteht also darin, dass man einem Attributnamen die Relation voranstellt, aus der das betreffende Attribut kommt.
R2 der beiden Relationen R1(A1, A2,…, An, B1, B2,…,Bk) und R2(C1, C2,…,Cm, B1, B2,…,Bk) mit k gleichbenannte Attributen B1, B2,…,Bk die Relation
mit den Attributen (A1, A2,…,An, R1.B1, R1.B2,…, R1.Bk, R2.B1, R2.B2,…,R2.Bk, C1, C2,…,Cm). Die Qualifizierung besteht also darin, dass man einem Attributnamen die Relation voranstellt, aus der das betreffende Attribut kommt.
Der zweite Ansatz besteht darin, als zusätzliche Operation der Relationenalgebra die Umbenennung einzuführen. Mit der Umbenennung sorgt man dafür, dass alle gleichbenannten Attribute in einer der beiden beteiligten Relationen vor einem Join so umbenannt werden, dass die beiden Relationen keine gleichbenannten Attribute mehr haben. Wir verwenden diesen zweiten Ansatz, weil er erstens die implizite Umbenennung, die beim ersten Ansatze stattfindet, explizit macht und zweitens bei Joins über rekursive Beziehungen (R1  R1) der erste Ansatz sowieso versagt.
R1) der erste Ansatz sowieso versagt.
Natural Join
Der sogenannte Natural Join entspricht im Wesentlichen dem im vorangegangenen Kapitel beschriebenen Join. Allerdings muss berücksichtigt werden, dass in den beiden Relationen, die gejoint werden sollen, mehrere gleichbenannte Attribute vorkommen können. Wenn dies der Fall ist, so findet nach dem Kreuzprodukt eine Selektion über alle Paare gleichbenannter Attribute statt, d.h. es werden nur die Datensätze selektiert, bei denen paarweise die Werte gleichbenannter Spalten gleich sind.
Dürfen gleichbenannte Attribute nicht zur Bestimmung des Natural Joins herangezogen werden, so benennt man diese Attribute in einer der beiden Relationen um.
Im Unterschied zu allen anderen Join-Varianten projiziert der Natural Join doppelt vorkommende Spalten aus.
Sind R1(A1, A2,…,An, B1, B2,…,Bk) und R2(C1, C2,…,Cm, B1, B2,…,Bk)
zwei Relationen mit den k gleichbenannten Attributen B1, B2,…,Bk,
so ist der Natural Join R1 ⨝ R2 eine Relation
mit den Attributen (A1, A2,…, An, B1, B2,…,Bk, C1, C2,…,Cm).
Haben R1 und R2 kein gemeinsames Attribut, so findet keine Selektion statt, aus dem Join wird ein Kreuzprodukt.
Equi Join
Theta Join
Der Theta-Join ist eine Verallgemeinerung des Equi-Joins. Als Selektionsbedingungen sind nicht nur Gleichheit, sondern auch andere Vergleichskriterien möglich. Beispiel:
Outer Join
Zur Erläuterung der Outer Joins verwenden wir eine Relation Artikel mit den Attributen ANr (Artikelnummer), Name des Artikels und KNr als Fremdschlüssel in die Relation Kategorie, welche ihrerseits die Attribute KNr (Kategorienummer) und Bezeichnung hat.
Artikel
| ANr | Name | KNr |
|---|---|---|
| 1 | Schokolade | 4 |
| 2 | Edamer | 1 |
| 3 | Tofu | NULL |
| 4 | Lachs | 2 |
Kategorie
| KNr | Bezeichnung |
|---|---|
| 1 | Milchprodukte |
| 2 | Meeresfrüchte |
| 3 | Getränke |
| 4 | Süßwaren |
Left Outer Join
Beim Left Outer Join werden alle Zeilen der linken Tabelle in die Ergebnisrelation übernommen. Fehlt bei einer Zeile der Join-Partner, wird mit NULL-Werten aufgefüllt.
| ANr | Name | KNr | KNr | Bezeichnung |
|---|---|---|---|---|
| 1 | Schokolade | 4 | 4 | Süßwaren |
| 2 | Edamer | 1 | 1 | Milchprodukte |
| 3 | Tofu | NULL | NULL | NULL |
| 4 | Lachs | 2 | 2 | Meeresfrüchte |
Right Outer Join
Beim Right Outer Join werden alle Zeilen der rechten Tabelle in die Ergebnisrelation übernommen. Fehlt bei einer Zeile der Join-Partner, wird mit NULL-Werten aufgefüllt.
| ANr | Name | KNr | KNr | Bezeichnung |
|---|---|---|---|---|
| 2 | Edamer | 1 | 1 | Milchprodukte |
| 4 | Lachs | 2 | 3 | Meeresfrüchte |
| NULL | NULL | NULL | 3 | Getränke |
| 1 | Schokolade | 4 | 4 | Süßwaren |
Full Outer Join
Beim Full Outer Join werden alle Zeilen der linken und rechten Tabelle in die Ergebnisrelation übernommen. Fehlt bei einer Zeile der Join-Partner, wird mit NULL-Werten aufgefüllt.
| ANr | Name | KNr | KNr | Bezeichnung |
|---|---|---|---|---|
| 1 | Schokolade | 4 | 4 | Süßwaren |
| 2 | Edamer | 1 | 1 | Milchprodukte |
| 3 | Tofu | NULL | NULL | NULL |
| 4 | Lachs | 2 | 2 | Meeresfrüchte |
| NULL | NULL | NULL | 3 | Getränke |
Umbenennung - Beseitigung gleichbenannter Attribute
Die Umbenennung (engl. rename, grie. Buchstabe rho ρ) als Operation der Relationenalgebra wird zur Lösung von Namenskonflikten bei Join-Operationen benötigt.
Gegeben sei die Relation R(A, B, C, D, E, F, …). Dann ist ρA→X, B→Y, D→Z(R) eine Umbenennung der drei Attribute A, B und D in X, Y und Z. Die Relation ρA→X, B→Y, D→Z(R) hat die Attribute (X, Y, C, Z, E, F, …).
Beispiel
Gegeben ist die Tabelle KursLehrerRaum
| KursNr | Lehrer | Raum |
|---|---|---|
| 11 | Müller | 123 |
| 12 | Schulze | 124 |
| 27 | Bauer | 14 |
| 15 | Maier | 14 |
| 17 | Maier | 17 |
| 3 | Zange | 211 |
Die Umbenennung ρKursNr→KursID, Lehrer→Name(KursLehrerRaum) erzeugt diese Tabelle:
| KursID | Name | Raum |
|---|---|---|
| 11 | Müller | 123 |
| 12 | Schulze | 124 |
| 27 | Bauer | 14 |
| 15 | Maier | 14 |
| 17 | Maier | 17 |
| 3 | Zange | 211 |
Mengenoperationen
Außer den drei wichtigen Operationen Selektion, Projektion und Join gibt es noch sogenannte Mengenoperationen, wie sie aus der Mengenlehre bekannt sind:
- Vereinigung
- Durchschnitt
- Differenz
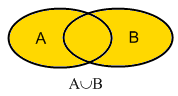
Vereinigung
Die Vereinigung A ∪ B zweier Relationen A und B besteht aus allen Datensätzen die in A oder B vorkommen.
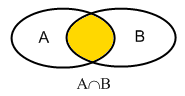
Durchschnitt
Der Durchschnitt A ∩ B besteht aus allen Datensätzen die sowohl in A als auch in B vorkommen.
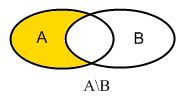
Differenz
Die Differenz A\B besteht aus allen Datensätzen die in A, aber nicht in B vorkommen.
Anwendung
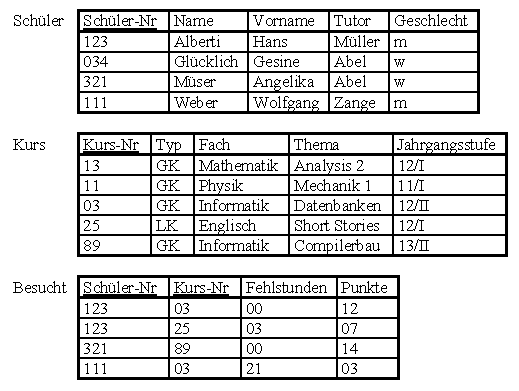
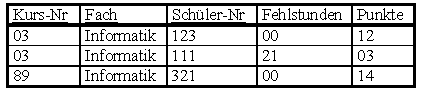
Zur Darstellung eines komplexeren Beispiels gehen wir von folgenden Tabellen einer Oberstufenverwaltung aus:
Es soll die Frage beantwortet werden, welche Mädchen Informatikkurse besuchen und welche Punktzahlen sie dabei erreicht haben.
1. Bestimmung der Informatikkurse
Informatikurse = πKurs-Nr(σFach = 'Informatik'(Kurs))
2. Join mit der Besucht-Tabelle über das gemeinsame Schlüsselattribut Kurs-Nr liefert die Informatik-Schüler:
Informatikschüler = Informatikkurse  Besucht
Besucht
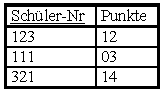
3. Projektion auf die benötigten Attribute Schüler-Nr und Punkte:
InformatikschülerPunkte = πSchüler-Nr, Punkte(Informatikschüler)
4. Join mit Schüler-Tabelle über das gemeinsame Schlüsselattribut Schüler-Nr.
InformatikschülerPunkteName = InformatikschülerPunkte  Schüler
Schüler
5. Selektion der Mädchen und Projektion auf die geforderten Angaben.
Ergebnis = πPunkte, Name, Vornameσ(Geschlecht = 'w'(InformatikschülerPunkteName))
6. Formal lässt sich die Berechnung der Anfrage durch folgenden Term der Relationenalgebra darstellen:
πPunkte, Name, Vorname(σGeschlecht = 'w'(πSchüler-Nr, Punkte(πKurs-Nr(σFach = Informatik(Kurs))  Besucht)
Besucht)  Schüler))
Schüler))
Aufgaben
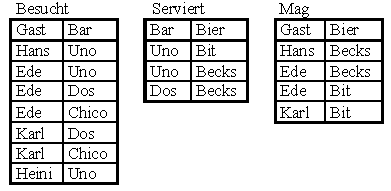
1. Gegeben seien drei Relationen:
a) Rekonstruiere das ER-Diagramm, aus dem die drei Relationen entstehen.
b) Bilde Serviert  Mag. Welche Informationen beinhaltet diese Relation?
Mag. Welche Informationen beinhaltet diese Relation?
c) Berechne mit einem Term der Relationenalgebra die Bars, die ein Bier servieren, das Karl mag.
d) Berechne die Biersorten, die in den besuchten Bars serviert werden.
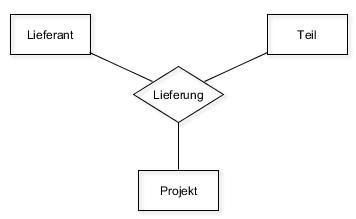
2. Gegeben seien folgende Relationen für drei Entitätstypen und eine ternäre Beziehung (# ist das Zeichen für Nummer):
Lieferanten(L#, LName, Status, Stadt)
Teile (T#, TName, Farbe, Gewicht, Stadt)
Projekte (P#, PName, Stadt)
Lieferungen (L#, T#, P#, Anzahl)
Hierbei bedeutet Stadt einmal die Stadt, in der ein Lieferant sitzt, die Stadt, in der das entsprechende Teil hergestellt wird, bzw. die Stadt, in der ein Projekt stattfindet. Löse die folgenden Aufgaben durch Operationen aus der Relationenalgebra:
a) Finde alle Lieferungen mit Anzahlen zwischen 300 und 750 und gib alle dazu in der Relation Lieferungen verzeichneten Informationen aus.
b) Gib alle Städte aus, in denen Lieferanten sitzen.
c) Gib alle vorkommenden Paarungen TName, Stadt aus.
d) Finde alle schwarzen Teile. Gib ihre Nummer und ihren Namen aus.
e) Finde alle Lieferanten, die in einer Einzellieferung mehr als 150 Teile geliefert haben. Gib ihren Namen aus.
f) Finde alle Teile, die von Lieferanten in London geliefert wurden. Gib davon die Teilenummer aus. Ändere so, dass der Teilenamen ausgegeben wird.
g) Finde alle Orte, in denen sowohl Projekte als auch Lieferanten beheimatet sind.
h) Finde alle Projekte, die mindestens einen Lieferanten für das Projekt im gleichen Ort haben. Gib die Projektnummer aus.
i) Finde alle Teile, die der Lieferant Lux geliefert hat. Gib alle Teilinformationen von diesen Teilen aus.
3. Gib Lösungen der Übungen 1 bis 5 zur Lektion 3 des [http://www.imoodle.de/sqltutorial/index.html |interaktiven SQL-Tutorials] als Terme der Relationenalgebra an.
4. Bestimme jeweils einen Relationenalgebraterm:
a) Für die rekursive Beziehung ist_Vorgesetzter_von mit der Relation Mitarbeiter(Personalnummer, Nachname, Vorname, ↑VorgesetztenPersonalnummer) sollen die Mitarbeiter, die den Vorgesetzten Paul Schmidt haben, bestimmt werden.
b) Es soll eine Relation mit Name und Vorname aller Mitarbeiter erzeugt werden, die zu jedem Mitarbeiter auch Name und Vorname des Vorgesetzten enthält.