Miniwelten

Das ER-Diagramm stellt den Datenbankentwurf grafisch anschaulich dar, als Mensch kann man den Entwurf gut überblicken. Der Computer kommt mit dieser Form nicht so gut zurecht. Er hat seine Daten lieber in Schrift- als in Grafikform. Für die maschinelle Aufbereitung eines ER-Diagramms setzen wir die Entitäts- und Beziehungstypen deshalb in Schriftform um.

In relationalen Datenbanksystemen wie z.B. MySQL, Access oder Paradox werden auch Beziehungen auf Relationen abgebildet. Dabei gilt folgende

Der Primärschlüssel dieser Relation besteht aus den beiden Primärschlüsseln der Entitätstypen. Im Falle von 1:n bzw. 1:1-Beziehungen genügt ein Primärschlüssel als Primärschlüssel der Relation. Bei 1:n-Beziehungen ist dies der Primärschlüssel der n-Seite. Die Primärschlüssel Schülernummer und Kursnummer sind nur zusammen genommen Primärschlüssel für die Relation belegt. Jeder der beiden Primärschlüssel ist für sich genommen ein sogenannter Fremdschlüssel, also ein Schlüssel in einer fremden Relation. Fremdschlüssel kennzeichnen wir mit einem Pfeil ↑, der dem Fremdschlüsselattribut voran gestellt wird.

Die Grundregel kann immer angewendet werden. Sie liefert unabhängig von der Kardinalität der Beziehung stets drei Relationen bei der Abbildung einer ER-Beziehung: je eine für die beiden beteiligten Entitätstypen und eine für die Beziehung.

Es gibt viele Fälle, in denen man mit weniger Relationen auskommt. Diese Fälle können bei 1:1 und 1:n-Beziehungen auftreten, aber nicht bei n:m-Beziehungen. Anhand von zwei Aufgaben betrachten wir Möglichkeiten Relationen und damit Tabellen beim Abbilden von ER-Beziehungen einzusparen.

Aufgabe 1
Jeder Oberstufenschüler hat einen Lehrer als Tutor.
a) Stelle die Tutor-Beziehung zwischen Schüler und Lehrer als ER-Diagramm dar.
b) Bilde gemäß der Grundregel auf Relationen ab.
c) Veranschauliche die Relationen mit ausgefüllten Tabellen.
d) Ermittle die Optionalität der Beziehung.
e) Reduziere die Verteilung der gesamten Information auf zwei Tabellen.
f) Vergleiche mit Aufgabe 2.
Lösung von Aufgabe 1

Aufgabe 2
Bücher können von Schülern ausgeliehen werden.
a) Stelle die hat-ausgeliehen-Beziehung zwischen Schüler und Buch als ER-Diagramm dar.
b) Bilde gemäß der Grundregel auf Relationen ab.
c) Veranschauliche die Relationen mit ausgefüllten Tabellen.
d) Ermittle die Optionalität der Beziehung.
e) Reduziere die Verteilung der gesamten Information auf zwei Tabellen.
f) Vergleiche mit Aufgabe 1.
Lösung von Aufgabe 2

Die beiden 1:n-Beziehungen unterscheiden sich hinsichtlich der Optionalität: jeder Schüler hat einen Tutor, aber nicht jedes Buch muss ausgeliehen sein. Im ersten Fall handelt es sich um eine obligatorische (muss) Beziehung, im zweiten um eine optionale (kann) Beziehung. Bei einer obligatorischen Beziehung gibt es keine sonderlichen Probleme, wenn drei Relationen zu zwei Relationen zusammengefasst werden.

Die beiden Grundregeln liefern diese drei Relationen:

Zur Optimierung integrieren wir den Primärschlüssel Kürzel der 1-Seite als Fremdschlüssel in die n-Seite. Dadurch wird eine Realtion eingespart.

Beim zweiten Beispiel treten Nullwerte auf, wenn man die Beziehungsrelation in die Relation der n-Seite integriert.

Bei einem nicht ausgeliehenden Buch bleibt der Fremdschlüssel Schülernummer leer. Man spricht in der Fachsprache von einem Nullwert. Das Attribut hat dann den Wert NULL. Sind viele Bücher da und nur wenige Bücher ausgeliehen, wird unnötig viel Speicherplatz für den zusätzlichen Fremdschlüssel verbraucht. Daher benutzen wir die folgende Regel:

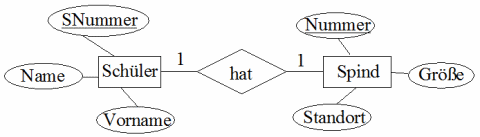
Wir betrachten die ER-Beziehung Schüler hat Spind.

Nach der Grundregel wird dieses ER-Diagramm auf drei Relationen abgebildet:

Lässt sich das Relationenmodell vereinfachen? Wir betrachten dazu vier unterschiedliche Fälle.

Fall A: Spinde an der Lichtenbergschule

An der Lichtenbergschule können Spinde von Schülern gemietet werden. Die Vertragsfirma hat so viele Spinde aufgestellt, wie Mietverträge abgeschlossen wurden. Jeder Spind gehört also zu einem Schüler, aber nicht jeder Schüler hat einen Spind. Die Beziehung ist also auf der Spind-Seite obligatorisch, weswegen die hat-Beziehung in die Spind-Seite integriert werden kann, ohne dass Nullwerte auftreten. Es reichen zwei Relationen aus:

Fall B: Spinde an einer amerikanischen Schule

An einer amerikanischen Schule hat jeder Schüler einen Spind, wegen der ständigen Fluktuation in der Schülerpopulation gibt es einige Spinde in Reserve. Jeder Schüler hat einen Spind, aber nicht jeder Spind ist genutzt. Die Beziehung ist also auf der Schüler-Seite obligatorisch und auf der Spind-Seite optional. Die hat-Beziehung kann in die Schüler-Relation integriert werden, ohne dass Nullwerte auftreten. Es reichen zwei Relationen aus:

Fall C: Spinde beim Bund

In einer Kaserne werden die Zimmer mit Rekruten voll belegt. Für jeden Rekruten gibt es genau einen Spind auf dem Zimmer. Die Rekrut-hat-Spind-Beziehung ist also auf beiden Seiten obligatorisch. In diesem Fall kommt man mit einer einzigen Relation aus:

Allerdings entspricht diese Relation nicht der 3. Normalform.

Fall D: Spinde im Schwimmbad

Gehen Schüler im Sommer ins Schwimmbad, so können sie einen Spind belegen. Bei kühler Witterung sind sicherlich nicht alle Spinde belegt. Die Schüler-Spind-Beziehung ist also auf beiden Seiten optional. Obwohl eine 1:1-Beziehung vorliegt, wird in diesem Fall nur dann eine Reduktion auf zwei Relationen vorgenommen, wenn die meisten Spinde belegt sind.

Wird zwecks Optimierung ein Primärschlüssel der Relation R₁ als Fremdschlüssel in die Relation R₂ aufgenommen, so tritt ein Namenskonflikt auf, wenn der Fremdschlüssel den gleichen Namen wie ein Attribut der Relation R₂ hat.

Im Beispiel Schulamt kommen diese beiden Relationen vor:

Die 1:n-Beziehung Klasse gehört zu Schule wird durch Hinzunahme des Primärschlüssels Name in die Relation Klasse abgebildet, wodurch der Namenskonflikt bei den Name-Attributen entsteht.

Ein Namenskonflikt wird dadurch aufgelöst, dass man den Fremdschlüssel geeignet umbenennt, am besten durch Hinzunahme des Namens der Relation. Im Beispiel nennt man demgemäß den Fremdschlüssel Name in Schulname um.

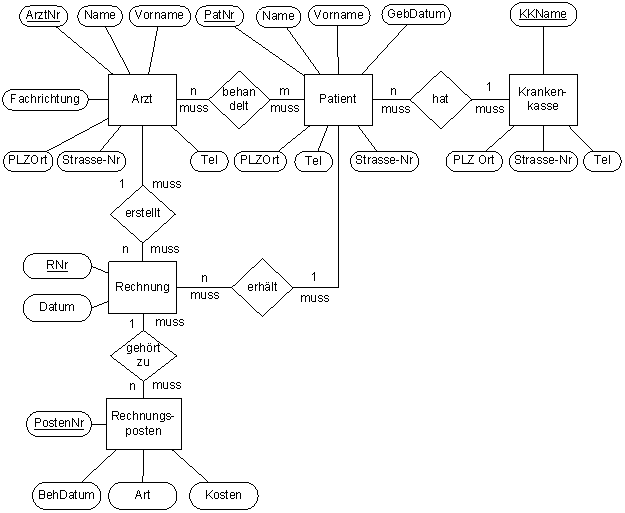
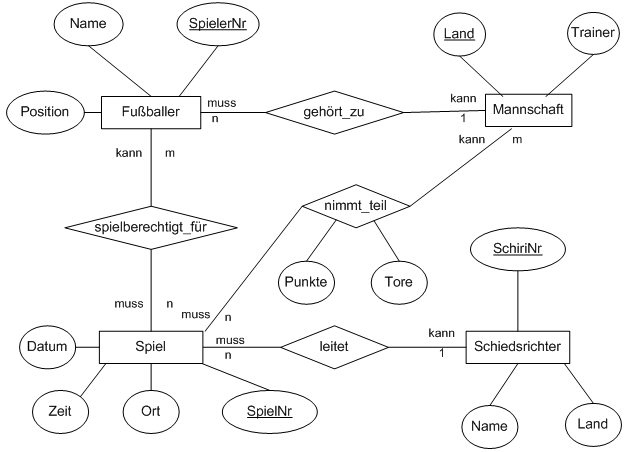
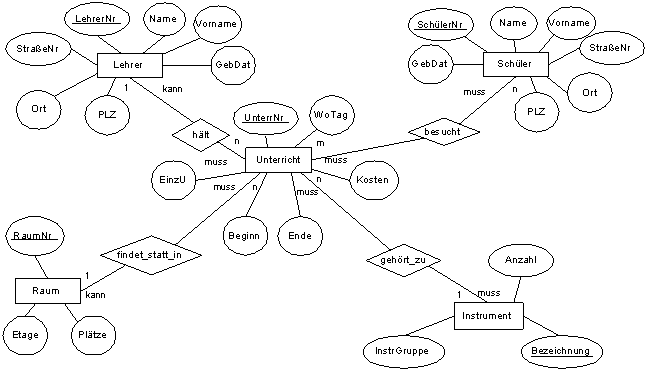
Nachfolgend sind drei ER-Diagramme gegeben.

sowie ein Dokument mit den drei ER-Diagrammen zum direkten Bearbeiten

a) Überführe die drei ER-Diagramme mit den beiden Grundregeln in nicht optimierte Relationenmodelle.
b) Optimiere die drei Relationenmodelle aus a).